
दोस्तो आज के इस article मे हम पढ़ेंगे की सरल सूक्ष्मदर्शी और संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता क्या है और इसका सूत्र क्या है एवं इसे सूत्रो को व्युत्पन्न करेंगे
सरल सूक्ष्मदर्शी की आवर्धन क्षमता
प्रतिबिम्ब देखने पर बना दर्शन कोण और स्पष्ट दृष्टि को दूरी पर रखी वस्तु को देखने पर बना दर्शन कोण के अनुपात को सरल सूक्ष्मदर्शी की आवर्धन क्षमता कहते है
सरल सूक्ष्मदर्शी कम फोकस दूरी का एक उत्तल लेंस होता है जो एक हैंडल लगे फ्रेम मे लगा होता है
सरल सूक्ष्मदर्शी की आवर्धन क्षमता कासूत्र-
अवर्धन क्षमता =प्रतिबिम्ब को देखने पर बना दर्शन कोण/वस्तु को देखने पर बना दर्शन कोण
m = β /α
∵ α व β का मान बहुत कम होता है
α = tanα , β = tanβ
m = tanβ/tanα ……..(1)
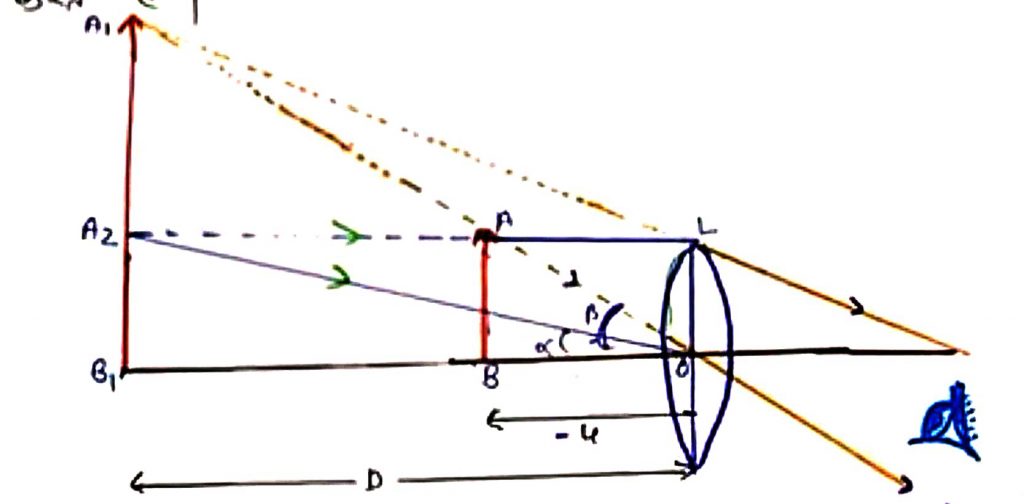
चित्र से-
tanα = B₁A₂/OB₁
∵ A₂B₁= AB
tanα = AB/OB₁
tanα = AB/D ……….(2)
tanβ = AB/OB ………(3)
tanα व tanβ का मान समी. मे रखने पर –
m = (AB/OB)/(AB/D)
m = D/OB
(∵ OB = -u)
m = D/-u
चिन्ह परिपाटी से-
m = D/u ……….(4)
Case 1. जब प्रतिबिंब स्पष्ट दृष्टि के न्युनतम दृष्टि पर बने-
लेंस सूत्र से-
1/f = 1/v – 1/u
चिन्ह परिपाटी से –
v = -D
u = – u
1/f = 1/-D – 1/-u
1/f = – 1/ D +1/u
दोनो पक्षो मे D से गुणा करने पर –
D/f = -D/D + D/u
D/f = – 1 + D/u
1 + D/f = D/u
समी. (4) से –
m = 1 + D/f
Case 2. जब प्रितिबिंब अंनंत पर बने
u = f , v = ∞
समी. (4) से –
m = D/ f
सयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता
अंतिम प्रतिबिम्ब को देखने पर बना दर्शन कोण और स्पष्ट दृष्टि की दूरी पर रखी वस्तु को देखने पर बना दर्शन कोण के अनुपात को सयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता कहते है
सयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता सूत्र-
आवर्धन क्षमता =अंतिम प्रतिबिम्ब को देखने पर बन दर्शन कोण/स्पष्ट दृष्टि की दूरी पर रखी वस्तु को देखने पर बना दर्शन कोण
m = β/α
α व β का मान बहुत कम होता है
α = tanα , β = tanβ
m = tanβ/tanα ……..(1)
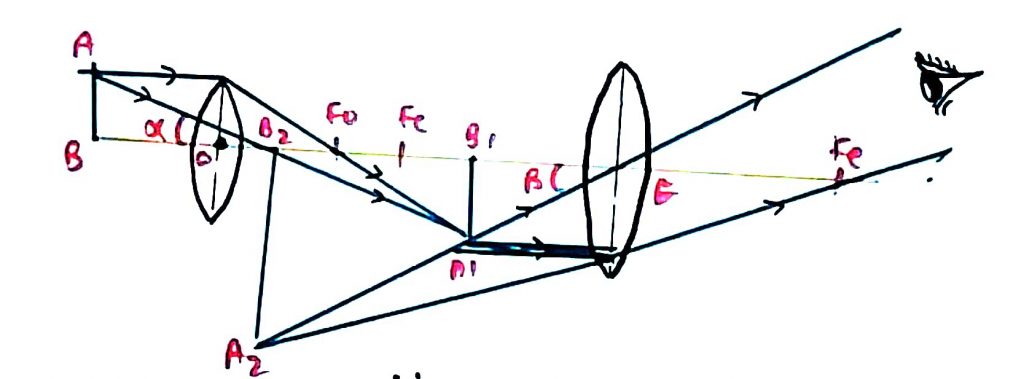
चित्र से –
वस्तु AB स्पष्ट दृष्टि के न्युनतम दूरी पर हो
tanα = AB /D
tanβ = A₁B₁/EB₁
समी. (1) मे मान रखने पर –
m = (A₁B₁/EB₁)/(AB/D)
m = A¹B¹/AB . D/EB₁ ……..(2)
ΔA₁OB₁ व ΔAOB समरूप है
A₁B₁/AB = OB
समी. (2) से –
m = OB₁/OB × D/EB₁ ……..(3)
चिन्ह परिपाटी से –
OB₁ = v₀
OB = -u₀
EB₁ = -ue
समी. (3) मे मान रखने पर –
m = v₀/-u₀ × ⁻D/-ue
m = -v₀/u₀ . D/ue ……..(4)
Case 1. जब प्रतिबिंब स्पष्ट दृष्टि के न्युनतम दूरी पर बने
लेंस सूत्र से –
1/f = 1/v – 1/u
चिन्ह परिपाटी से –
1/fe = 1/-D – 1/-ue
1/f = 1/-D + 1/ue
दोनो पक्षो मे द से गुणा करने पर –
D/fe = D/-D + D/ue
D/ fe = – 1 + D/fe
समी. (4) से –
m = -v₀/u₀(1+ D/fe) ……(5)
Case 2. जब प्रतिबिंब अनन्त पर बने –
ue = fe
समी. (4) से –
m = -v₀/u₀ . D/fe
आशा है सूक्ष्मदर्शी की आवर्धन क्षमता आपको समझ आ गया होगा कोई प्रश्न हो तो कमेंट में लिखें और इस पेज को शेयर जरूर करें

Leave a Reply